第1课时平面向量的实质背景及基本定义
基础达标
1.下列说法正确的是.
A.有向线段
与
表示同一向量
B.两个有公共终点的向量是平行向量
C.零向量与单位向量是平行向量
D.对任意向量a,
是一个单位向量
【分析】向量与方向相反,不是同一向量,A错误;有公共终点的向量的方向未必相同或相反,B错误;当a=0时,无意义,D错误;零向量与任何向量都是平行向量,C正确.
【答案】C
2.下列说法中不正确的是.
A.向量的长度与向量的长度相等
B.任何一个非零向量都可以平行移动
C.长度不相等而方向相反的两个向量肯定是共线向量
D.两个有一同起点且共线的向量其终点必相同
【分析】两个有一同起点且共线的向量,它们的方向可能相反,而且它们的长度也大概不同,所以D不正确.
【答案】D
3.如图,梯形ABCD为等腰梯形,则两腰上的向量
与
的关系是.
A.=
B.||=||
C.>
D.<
【分析】||与||表示等腰梯形两腰的长度,故相等.
【答案】B
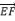
4.如图,在四边形ABCD中,=,则相等的向量是.
A.
与
B.
与
C.
与
D.与
【分析】由=知四边形ABCD是平行四边形.由平行四边形的性质知,||=||,且方向相同,故选D.
【答案】D
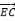
5.如图,四边形ABCD和四边形ABDE都是平行四边形.
与向量
相等的向量有__________;
若||=3,则向量的模为__________.
【分析】在平行四边形ABCD和ABDE中,=
,=,∴=.
由知=,∴||=||+||=2||=6.
【答案】,6
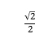
6.如图,
是某人行走的路线,那样的几何意义是某人从A点沿西偏南__________方向行走了__________km.
【答案】60°2
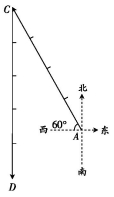
7.请画出下列表示小船的位移的图形.
由A地向东北方向航行15 km到达B地;
由A地向西偏北60°方向航行20 km到达C地;
由C地向正南方向航行25 km到达D地.
【分析】如图所示,按1∶500000的比率尺画图
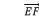
见图中位移
.
拓展提高
8.下列说法正确的个数是.
①两个有公共起点且长度相等的向量,其终点可能不同;
②若非零向量与是共线向量,则A,B,C,D四点共线;
③若a∥b且b∥c,则a∥c;
④当且仅当=时,四边形ABCD是平行四边形.
A.0 B.1 C.2 D.3
【分析】①正确;
②不正确,由于向量的共线与表示向量的有向线段共线是两个不一样的定义;
③不正确,假设向量b为零向量,由于零向量与任何一个向量都平行,符合a∥b且b∥c的条件,但结论a∥c却未必成立;
④正确,由于四边形ABCD是平行四边形⇔AB∥DC且AB=DC,即和相等.
【答案】C
9.如图,在等腰三角形ABC中,∠C=90°,CD⊥AB,则下列结论正确的是__________.
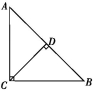
①是单位向量;
②||=
||;
③∥
;
④∥.
【分析】由图可知,显然
与不平行,与不平行,所以③④不正确.又由于等腰三角形ABC的边长不确定,所以不可以确定是不是为单位向量,所以①不正确.依题意,知CD=BC,所以②正确.
【答案】②
10.在等腰梯形ABCD中,AB∥CD,对角线AC与BD相交于点O,EF是过点O且平行于AB的线段,其与两腰分别交于点E,F,在图中所标的向量中:
写出与共线的向量;
写出与方向相同的向量;
分别写出与
,
的模相等的向量;
写出与
相等的向量.
【分析】在等腰梯形ABCD中,AB∥CD∥EF,AD=BC.
图中与共线的向量有,
,,.
图中与方向相同的向量有,,,.
图中与的模相等的向量为
,与
的模相等的向量为.
图中与相等的向量为.
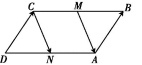
11.如图所示,在四边形ABCD中,=,N,M分别是AD,BC上的点,且
=.
求证:
=.
【分析】∵=,
∴||=||,且AB∥CD,∴四边形ABCD是平行四边形.
∴|
|=||,且DA∥CB.
又∵与的方向相同,∴=.
同理可证四边形CNAM是平行四边形,∴
=.
∵||=||,||=||,
∴||=|
|,DN∥MB,即与的模相等且方向相同,∴=.
